CMU 11611 的课程笔记。讲句法的相关概念及各种 parsing 算法包括 CFG / PCFG / CKY / Earley 等。
Context-Free Grammars
我们怎么知道哪些单词可以组合在一起(形成一个成分)呢?一个明显的依据是它们都可以出现在相同的句法环境中。Context-Free Grammar,简称 CFG,又称短语结构语法(Phrase-Structure Grammar),形式化方法等价于Backus-Naur范式(Backus-Naur Form,简称BNF)。
CFG 对形式语言(formal language)进行了限制,production rule 箭头(→)左边只能是一个 non-terminal symbol,表示某种聚类或概括性,右边的项是一个或多个 terminal 和 non-terminal 符号构成的有序表,可以把 CFGs 想象成句子的 generator,那么可以把“→”读为“用右边的符号串来重写左边的符号”。定义如下:
- N: a set of non-terminal symbols
- $\Sigma$: a set of terminal symbols
- R: a set of production rules of the form $X \ → \ Y_1Y_2Y_n$ for n>=0, $X \in N$, $Y_i \in (N \cup \Sigma)$
- $S \in N$: a distinguished/special start symbol
来个例子
我们可以把 CFGs 想象成 declarative programs,像是 Prolog, SQL, XQuery,Re,只声明最后想要做什么(ultimate goal),而不是怎么做(intermediary steps),也就是说相同程序可以被用在各种不同的 context 下面,而命令式编程(imperative programs)则是基于上下文的。
CFGs specify what is to be computed in terms of rules and let generalized computation mechanisms solve for the particular cases
判断一些语言是不是 Context-Free Grammar
CFG 有两个相关任务,一个是 Recognition(识别),一个是 Parsing(剖析),输入与输出如下:
- Input: sentence w=(w1,…,wn) and CFG G
- Output(recognition): true iff $w \in Language(G)$
- Output(parsing): one or more derivations for w, under G
可以用 Earley 算法在 O(n^3) 的时间复杂度内识别 CFG,下面会具体介绍。
Chomsky Normal Form(CNF)
FSA and CFG
当一个 non-terminal 符号的展开式中也包含了这个 non-terminal 符号时,就会产生语法的递归(recursion)问题,如 Norminal → Norminal PP中,就有递归问题。
Chomsky(1959)证明了一个上下文无关语言(L)能够被有限自动机(FSA)生成,当且仅当存在一个生成语言 L 的、没有任何中心-自嵌入(center-embedded)递归的上下文语法($A→\alpha A \beta$)
之后会讨论 FSA 的一个扩充版本,递归转移网络(recursive transition network,简称 RTN),它给 FSA 增加了很强的地柜能力。由 RTN 形成的自动机恰好与上下文无关语法同构(isomorphic),在一定场合下,可以作为研究 CFG 的一个有用的比喻。
L(G) 是一种 push-down automata,可以被 normalized(Chomsky normal form)
- Chomsky normal form
- Only one or two symbols on RHS
CNF
让各个语法都拥有一个标准的形式非常有用(语法的规则部分都采用一种特殊的形式)。CNF 就是这样一种标准形式。如果一个 CFG 是 ε-free ( ε 表示空串),而且它的 rules 只有如下两种形式之一,且 $X, Y, Z \in N, \ w \in T$,那个这个 CFG 就是采用 CNF 形式的。CNF 语法都是二分叉的。
- X → Y Z
- X → w
Transformation
任何语法都可以转化成一个弱等价的 CNF 形式,只改变树的结构,且能识别相同的语言。基本思路如下:
- Empties and unaries are removed recursively
- n-ary rules are divided by introducing new nonterminals(n>2)
CFGs 到 CNF 的转化过程:
- For each rule
X → A B C - Rewrite as
X → A X2
X2 → B C
相当于引入了一个新的 non-terminal
一个上下文无关语法 $G=(N, \Sigma, R, S)$ 在 Chomsky Normal Form 下的表达如下:
- N: a set of non-terminal symbols
- $\Sigma $: a set of terminal symbols
- R: a set of rules which take one of two forms:
X → $Y_1Y_2$ for X $\in$ N, and $Y_1Y_2 \in N$
X → Y for X $\in$ N, and Y $\in \Sigma$ - $S \in N$: distinguished start symbol
E.g.
Binarization
Binarization is crucial for cubic time CFG parsing.
这是我们必须知道的一条法则,在高效的 CFG parsing 中,Binarization 几乎总是必不可少的,可能是在 parsing 算法之前(如 CKY),也可能是隐藏在了 parsing 算法中,但它总会被用到。
看一下 binarization 之前的 parse tree,VP → V NP PP 这一条是不符合 CNF 规则的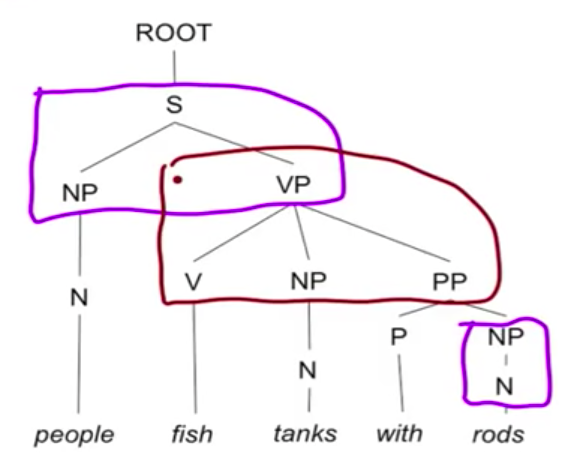
添加新的 non-terminal @VP_V,进行 binarization 之后的 parse tree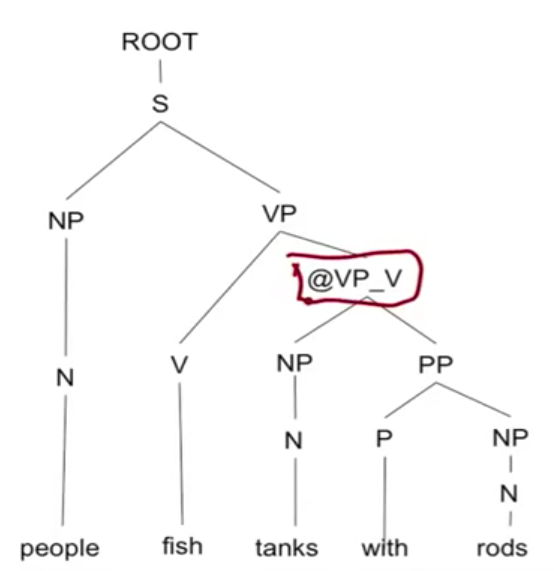
Unaries/Empties
进一步讨论下 unaries/empties,处理过程如下: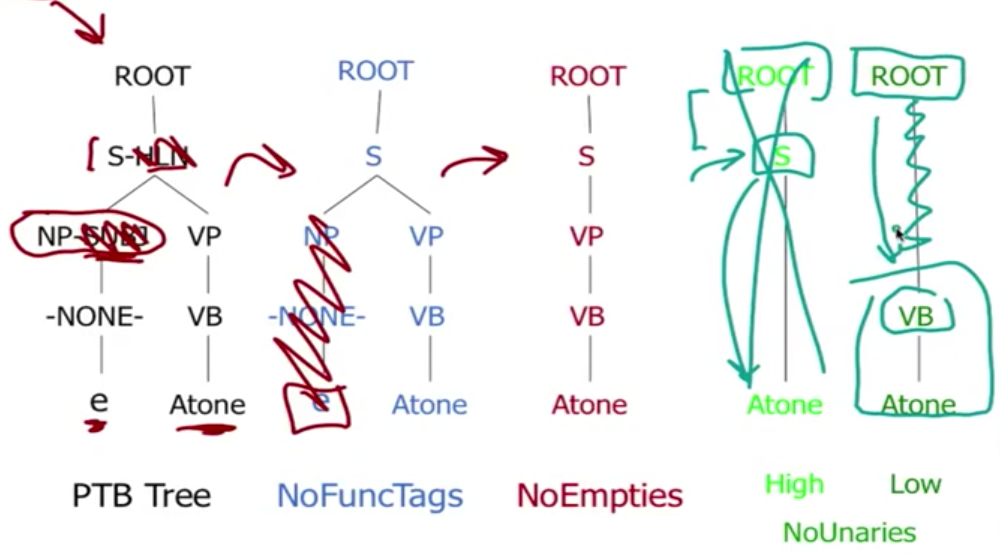
对 CNF 来说,重建 n-aries 是非常容易的,然而重建 unaries/empties 就非常的 tricky 了,一个 neat and clean 的 CNF 往往需要删除 empties and unaries,但另一方面,我们也可以简单的保留它们(通常只删除 emptie,保留 unaries,如上图的 non-empties 的树),以便能够重建原来的 tree。
Recognition
把识别当作一个搜索来做,算法如下非常简单:
Parsing
上下文无关语法最后能产生剖析树(parse tree),这里看一下输入输出以及产生的信息,下面具体介绍 parse 过程。
INPUT: The burglar robbed the apartment.
OUTPUT: 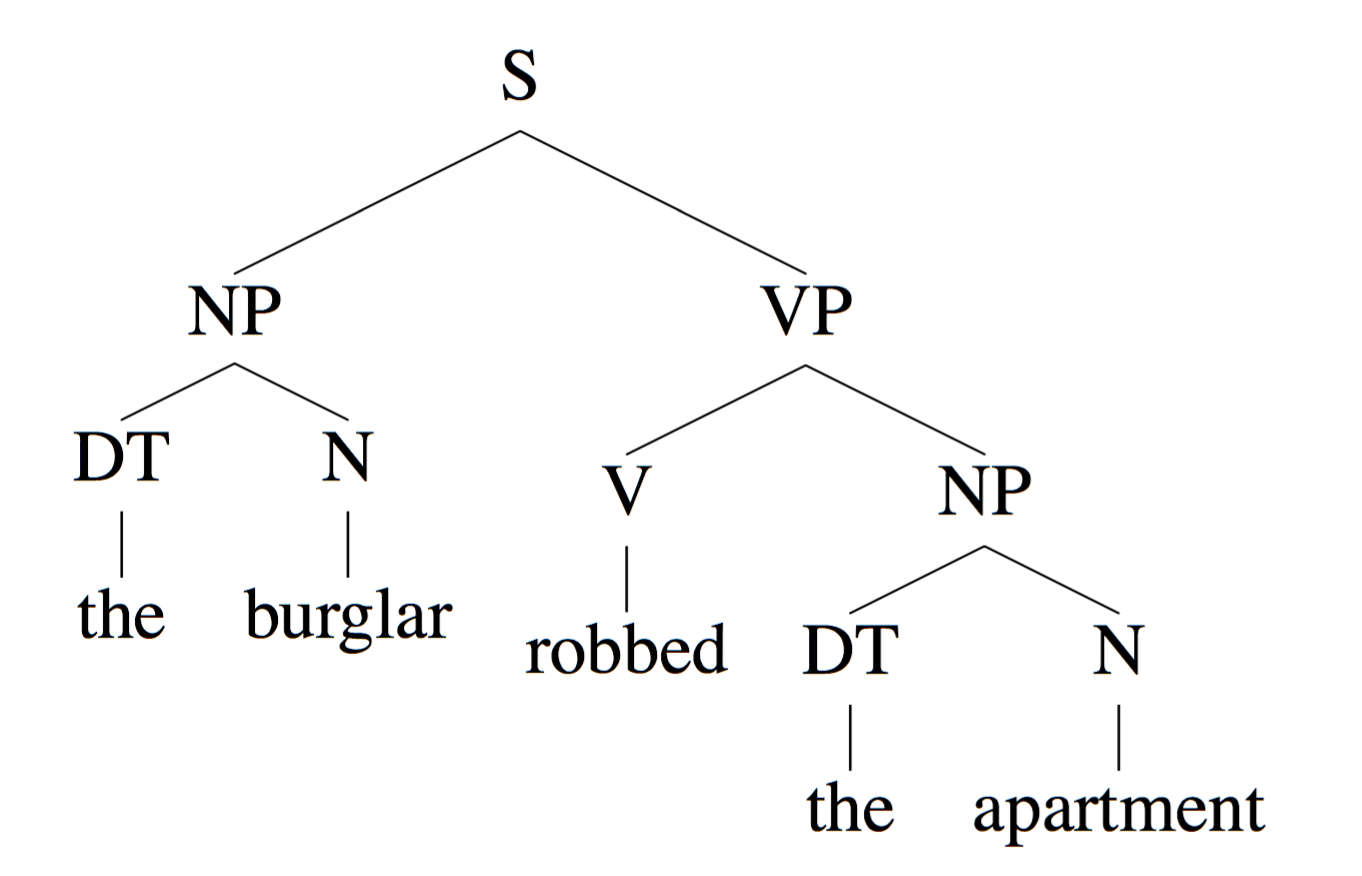
Parse Trees 可以传达的信息
- Part of speech for each word
N = noun, V = verb, DT = determiner - Phrases
Noun Phrases (NP): “the burglar”, “the apartment” VerbPhrases(VP): “robbedtheapartment”
Sentences (S): “the burglar robbed the apartment” - Useful Relationships
“the burglar” is the subject of “robbed”, see picture below
Application: Machine Translation
E.g. English word order: subject-verb-object, Japanese word order: subject-object-verb
|
|
Parsing 的算法有两类,一个是 top-down,一个是 bottom-up。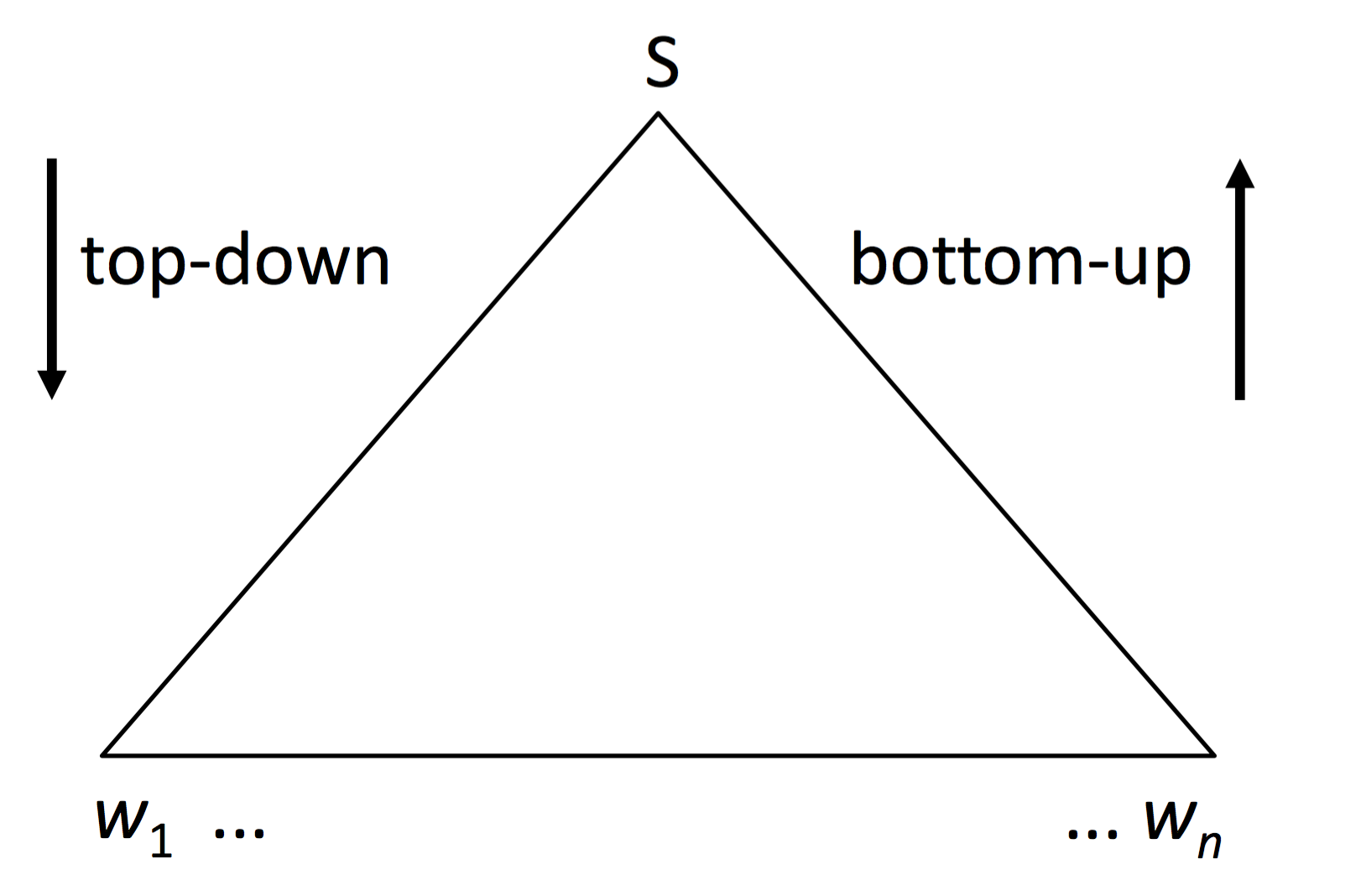
Top-down Parser
- Start state: (S, 0)
- Scan: From (wj+1 β, j), you can get to (β, j + 1).
- Predict: If Z → γ, then from (Z β, j), you can get to (γβ, j).
- Final state: (ε, n)
假定剖析要并行地构造出所有可能的树。算法开始时假定,给初始符号指派 S,输入就可以从 S 开始被推导出来。下一步搜索所有能够以 S 为顶点的树,寻找在语法的所有规则中左手边为 S 的规则。如下图,原始句子为 Book that flight,有三条规则可以展开 S,所以在图中的搜索空间第二层中,创造了三个局部树。
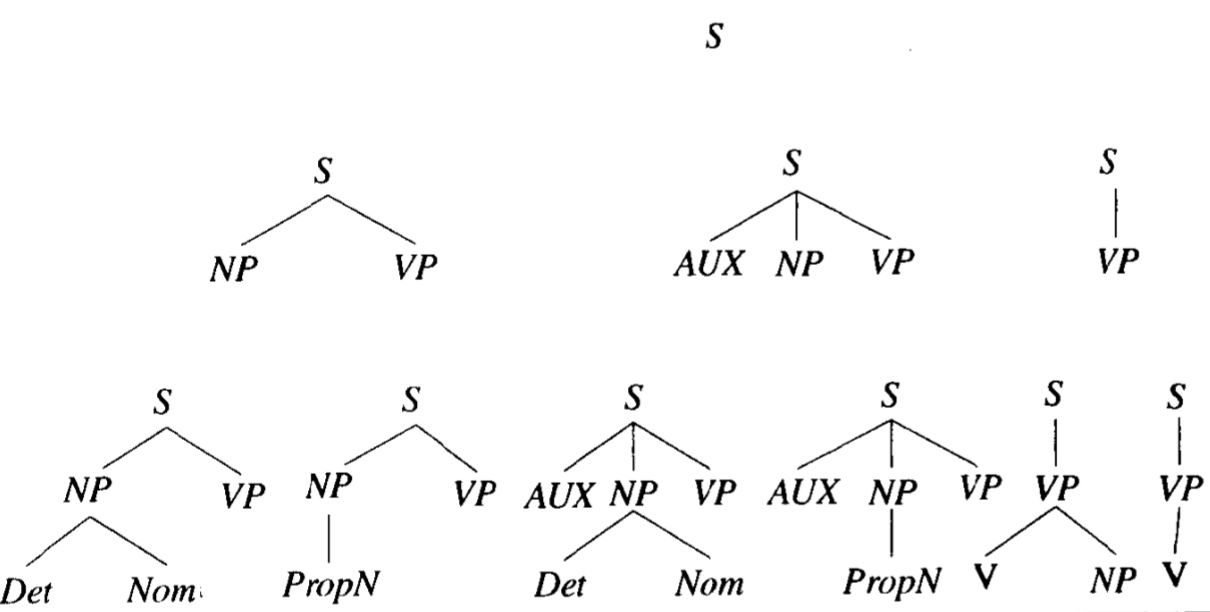
在第三层中,只有第五个 parse tree(由规则 VP → Verb NP 展开的树)最后与输入句子 Book that flight 相匹配。这里用的是 Left-Most Derivations 方法,每次都从最左边的 non-terminal X 开始,把 X 替换成 $\beta$($X→\beta$ 是 R 里的一条规则),再举一个例子:
E.g.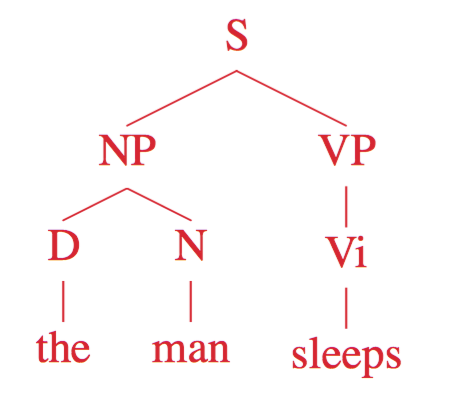
[S], [NP VP], [D N VP], [the N VP], [the man VP], [the man Vi], [the man sleeps]
Bottom-up Parser
- Start state: (ε, 0)
- Shift: From (α, j), you can get to (α wj+1, j + 1).
- Reduce: If Z → γ, then from (αγ, j) you can get to (α Z, j).
- Final state: (S, n)
从输入的单词开始,每次都是用语法中的规则,试图从底部的单词向上构造剖析树。如果剖析器成功地构造了以初始符号 S 为根的树,而且这个树覆盖了整个输入,那么剖析就获得了成功。同样,以 Book that flight 为例,book 有歧义,可能是动词也可能是名词,所以就有了刚开始的分叉。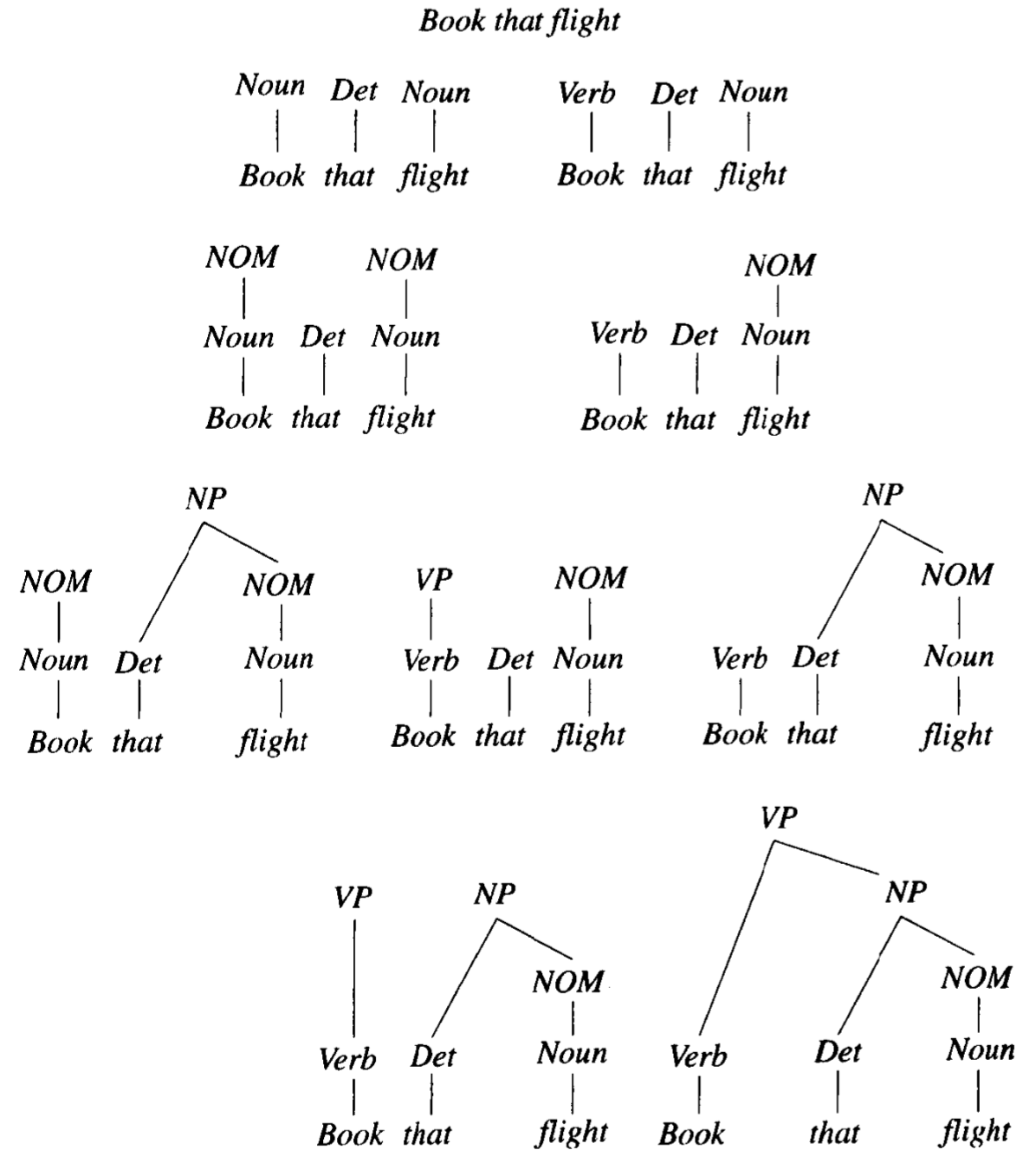
对于 bottom-up 的剖析,从一层到下一层时,要寻找被剖析的成分是否与某个规则的右手边相匹配,这与 top-down 的剖析正好相反。最后第二层,把 book 解释为名词的树枝在搜索空间中被剪除,因为语法中没有以 Nominal NP 为右边的规则,因而无法继续剖析。
Top-down vs Bottom-up
两种方法各有优缺点。Top-down 策略绝不会浪费时间搜索一个不可能以 S 为根的树,或者说,它不可能去搜索那些在以 S 为根的树中找不到位置的子树;与此相反,bottom-up 策略中,那些不可能导致 S 的树大量存在着,如上面的例子,刚开始就把 book 错误的解释为名词,而在给定语法中,这样的树根本不可能推导出 S。
另一方面,top-down 会花费大量努力去产生与输入不一致的根为 S 的树,在 top-down 的图中,第三层六个树里,前四个树的左分支都不能与 book 匹配,因而这些树都不能形成最后的 parse tree。top-down 的这个弱点是由于这种方法在没有检查输入符号之前就开始生成树了,反之,bottom-up 绝不会去搜索那些不是以实际的输入为基础的树。
由此可见,这两种方法都不能有效利用语法和输入单词中的约束条件。
总而言之,Parsing 要解决的两个问题,一个是怎么 avoid repeated work,另一个是怎么解决 ambiguity。
Ambiguity
由 CFG 产生的字符串可能有多个 derivation,这就会产生 ambiguity。
E.g.
VP → Verb NP prefer a morning flight
VP → Verb NP PP leave Boston in the morning
VP → Verb PP leaving on Tuesday
如上,一个 VP 可能有多个规则,因此一个句子也可能有多个 parse tree。
Ambiguity 的来源:
- Part-of-Speech ambiguity
NNS → walks
Vi → walks - Prepositional Phrase Attachment
the fast car mechanic under the pigeon in the box
关于 attachment 带来的 ambiguity,再多讲几句,放在不同的地方修饰不同的词差别是很大的,一个 Prepositional Phrase(PP) 可以跟在前面的名词/动词前面,这就会产生各种歧义。
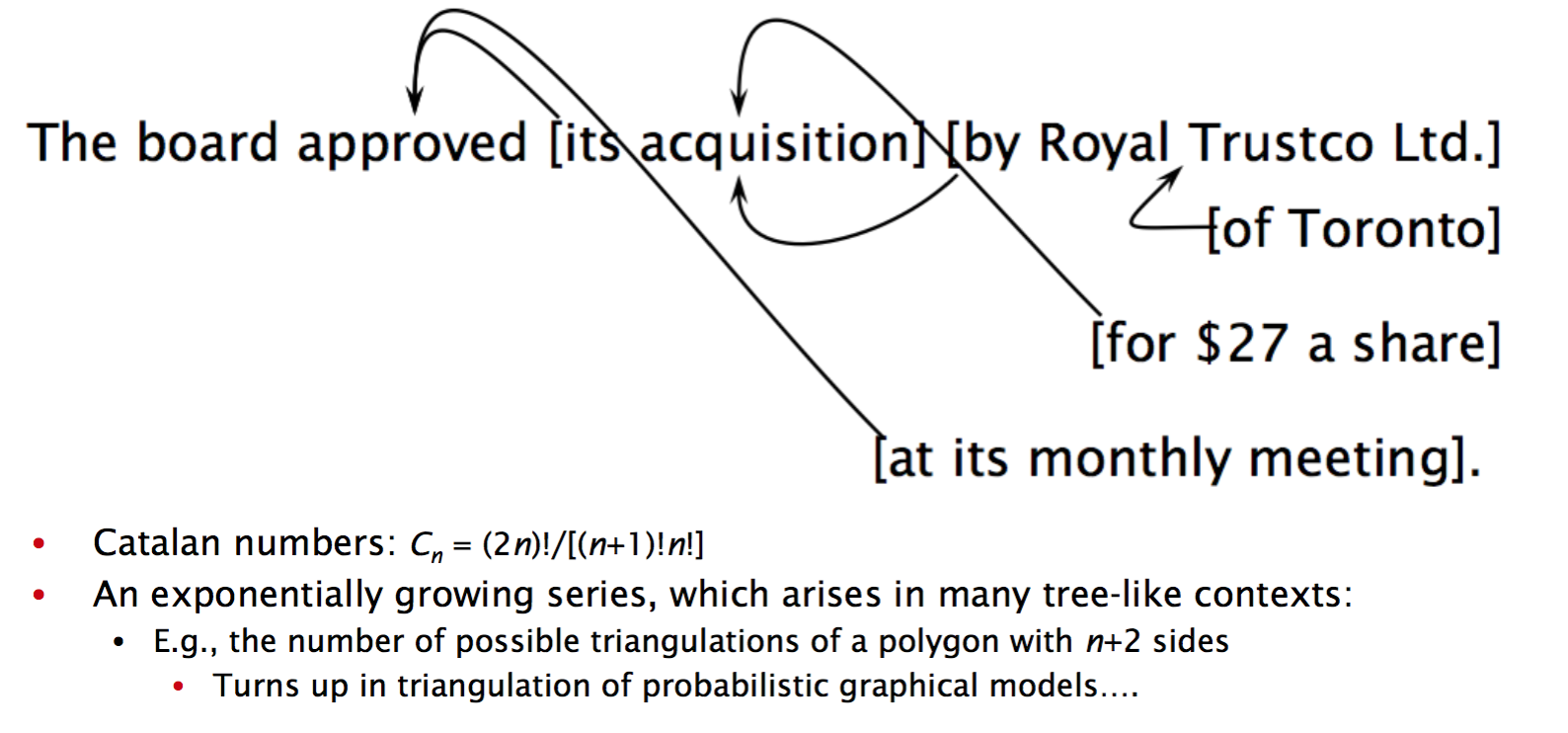
怎么选择正确的 parse 呢?有一种方法是基于统计数据,在语料库中,看某个 PP 跟在特定名词/动词后面的概率,取概率大的那种 parse。
Grammaticality
从语法而言,也有很多种表达,虽然下面的句子有些在我们看来语法上是错误的,然而表达上却是没有问题的
Summary
- CFG 提供了一个用于创建语法的工具集
Grammars that work well (for a given application)
Grammars that work poorly (for a given application) - 关于CFG理论,没有一个先验 prior 来告诉你给定应用的“正确”语法看起来应该是怎样的
- 一个好的语法通常是:
Doesn’t over-generate very much (high precision)
Doesn’t under-generate very much (high recall) - 在实践中具体情况具体分析
- CFG可能不足以完全捕获自然语言的语法
but almost adequate
computationally well-behaved
not very convenient as a means for hand- crafting a grammar
not probabalistic - 有些信息抽取问题可以不使用完全剖析,而使用层叠式 FSA(cascade)来解决
Improved Algorithms
Probabilistic Context-Free Grammar(PCFGs)
对 CFG 的最简单的提升就是概率上下文无关语法(PCFG),又称随机上下文无关语法(Stochastic Context-Free Grammar,简称 SCFG),其最大贡献是它进行了歧义消解(disambiguation),来自 Stanford 讲义
上下文无关语法 G 是由四个参数 (N,$\Sigma$, R, S)来定义的
- N: a set of non-terminal symbols
- $\Sigma$: a set of terminal symbols
- R: a set of production rules of the form $A \ → \ \beta$, $A \in N$, $\beta \in (N \cup \Sigma)$
- $S \in N$: a distinguished/special start symbol
PCFG 的产生式 R 中的每个规则都加上来一个条件概率,从而增强了这些规则:
$$A → \beta [p]$$
所以 PCFG 是一个五元组 (N,$\Sigma$, P, S, D),D 的功能是给 R 中的每个规则指派一个概率,或者说是把给定的 non-terminal 符号 p 展开为符号序列 $\beta$ 时的概率,这个概率通常表示为 $P(A → \beta)$,或者 $P(A → \beta|A)$,一个 non-terminal 符号的所有展开,概率之和为1.
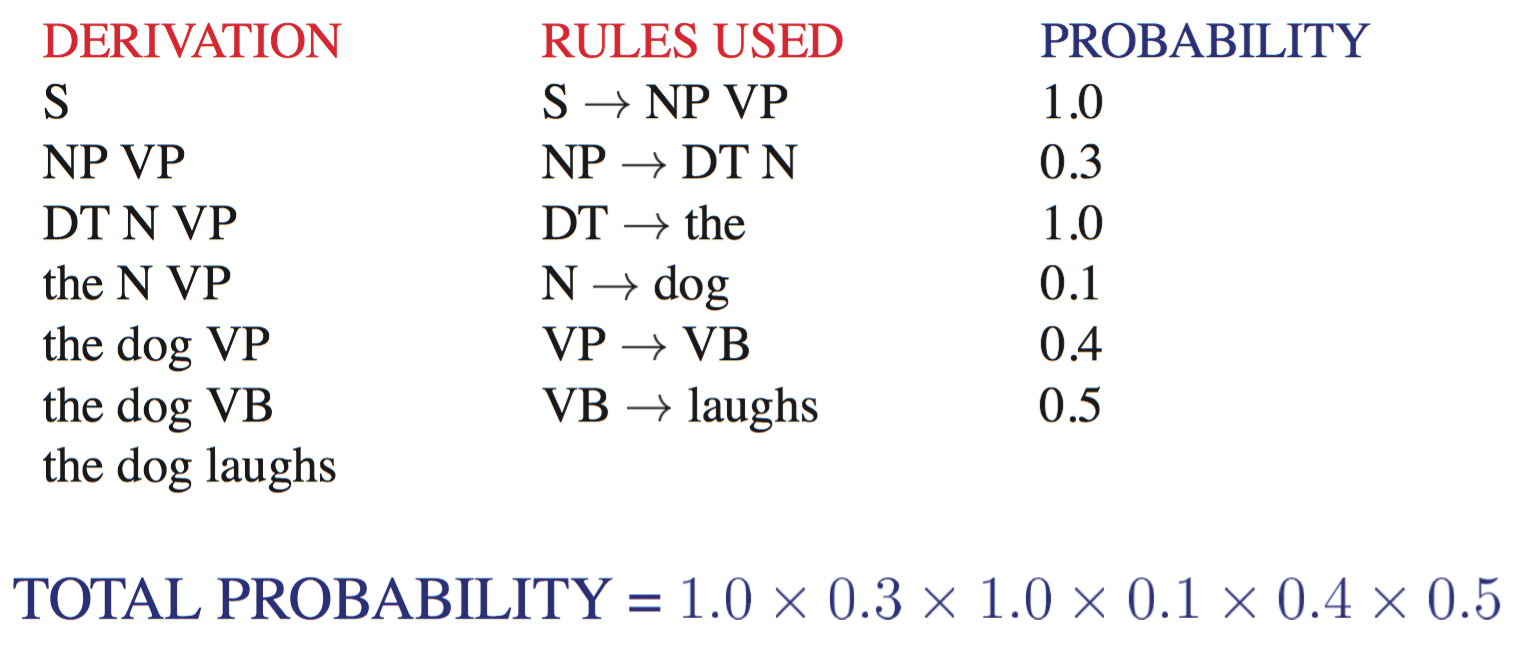
PCFG 可以用来估计关于一个句子及其 parse tree 的有用概率的数量。PCFG 可以对于一个句子 S 的每个 parse tree T(也就是每个推导结果)都指派一个概率,这在歧义消解(disambiguation) 中是非常有用的。
一个特定 parse tree T 的概率定义为在该 parse tree 中用来展开每个节点 n 的所有规则 r 的概率的乘积:
$$P(T,S)=\prod_{n \in T} p(r(n))$$
所以作为结果的概率 P(T,S)既是剖析和句子的联合概率,又是剖析 P(T)的概率。这是 make sense 的,因为剖析包含了句子中的所有单词,所以 P(S|T)=1,所以有
$$P(T,S)=P(T)*P(S|T)=P(T)$$
歧义消解(disambiguation)例子:
算出 $P(T_l)=1.5*10^{-6}$,$P(T_r)=1.7*10^{-6}$,右侧的 parse tree 具有比较高的概率,所以如果歧义消解算法选择具有最大 PCFG 概率的剖析,那么这个剖析便可以通过这样的歧义消解算法选择正确的结果。
形式化一下,得到给定句子 S 的最佳 parse tree T
$$
\begin{aligned}
\hat T(S) &= argmax_{T \in \tau(S)} P(T|S) \\
& = argmax_{T \in \tau(S)} {P(T|S) \over P(S)} \\
& = argmax_{T \in \tau(S)} P(T, S) \\
& = argmax_{T \in \tau(S)} P(T) \\
\end{aligned}
$$
$$P(S) = \sum_{T \in \tau(S)} P(T,S) = \sum_{T \in \tau(S)} P(T)$$
在 PCFG 中,如果一种语言的所有句子的概率之和为 1,就可以说这个 PCFG 是坚固的(consistent),有些递归规则会使语法变得不坚固,如概率为 1 的规则 S→S 就会导致概率量的丧失,因为推导永远不会终止。
PCFG 是 robust 的,它考虑了所有的可能,虽然通常带来了很低的概率;它部分解决了 grammar ambiguity 的问题,但并没有那么完美,因为它的独立性假设太强了;同时,PCFG 给出了一个基于概率的语言模型(probabilistic language model),然而它往往比 trigram model 的表现差的多,因为它缺少 lexicalization
另外,PCFG 假设任何一个 non-terminal 符号的展开与任何其他 non-terminal 符号的展开是独立的,然而这个假设太强了,可以通过 state-splitting 的方式来放宽假设,如下面的 Parent Annotation Tree 和 Marking possessive NPs Tree。同时要注意的是,如果分割太多了,可能会导致稀疏性问题。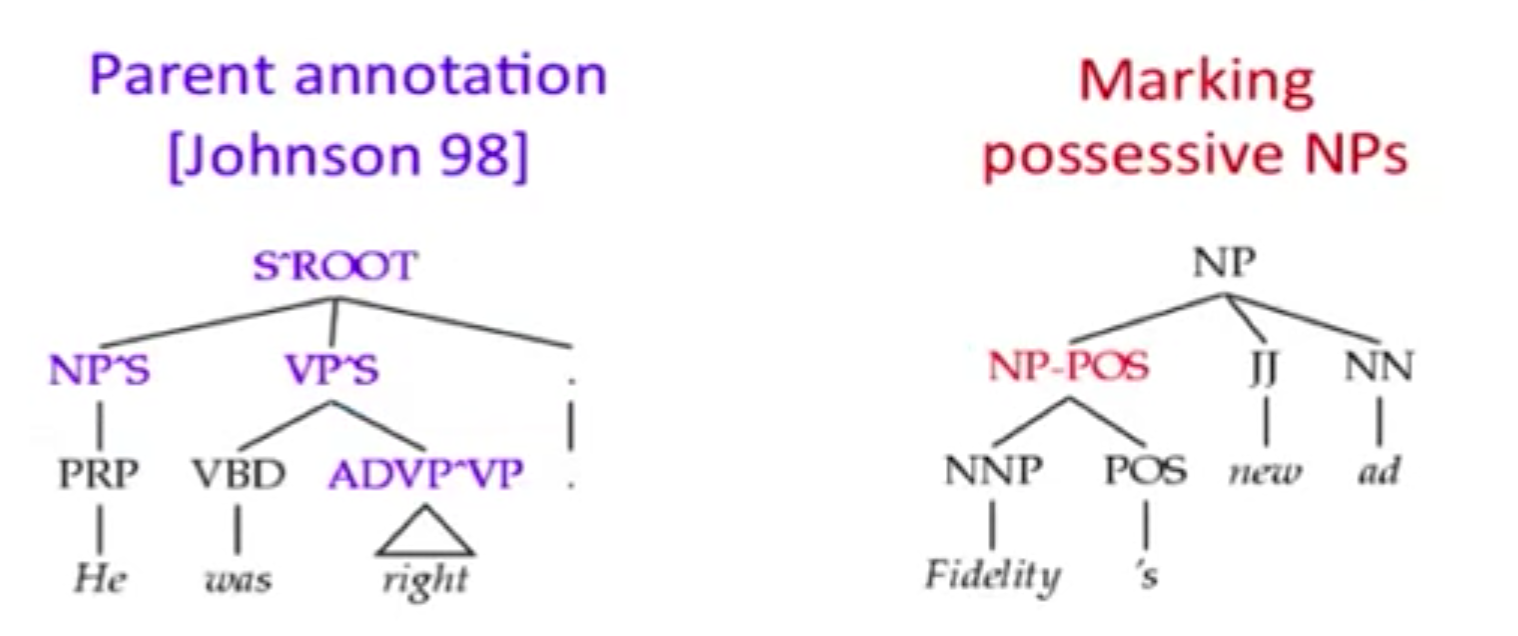
Cocke-Kasami-Younger
主要是一种 bottom-up 的剖析算法,使用动态规划表来存储结果。输入必须是具有 Chomsky 范式(CNF)的。以 People fish tanks 这个句子,形象化的理解 PCFG 下的 CKY 算法。首先为一个句子建立一个三角形的表格,然后 bottom-up 一层一层向上填充 chart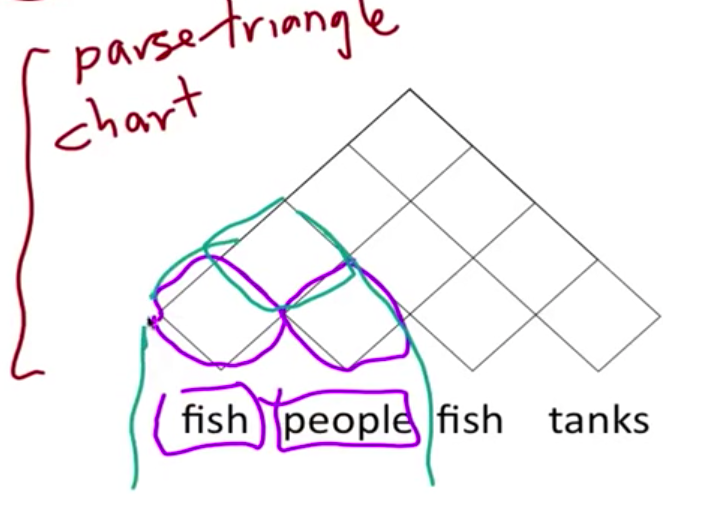
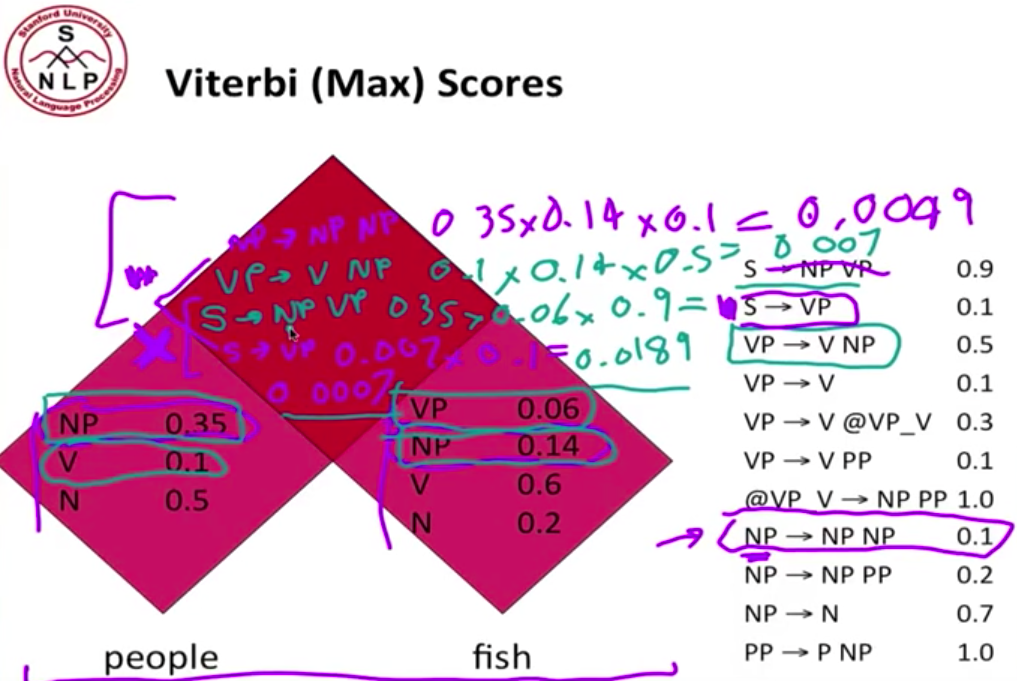
以前两个单词为例,假定单词的 PoS 已经填充完毕,现在我们要填充最上面的 cell。根据右边的规则找出所有可能的组合,计算概率。注意,如果规则的等式左边是 S,我们只保留最大概率的那个组合。在这个例子里,我们看到有两个可能性能够组成 sentence,S → NP VP 和 S → VP,这种情况下,我们只S → NP VP。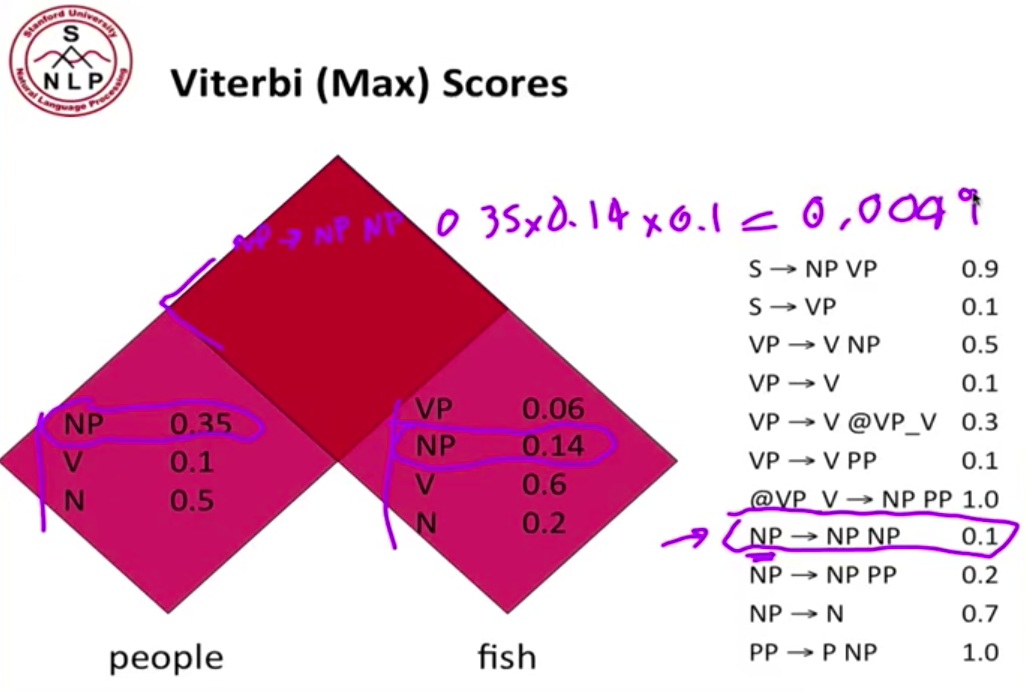
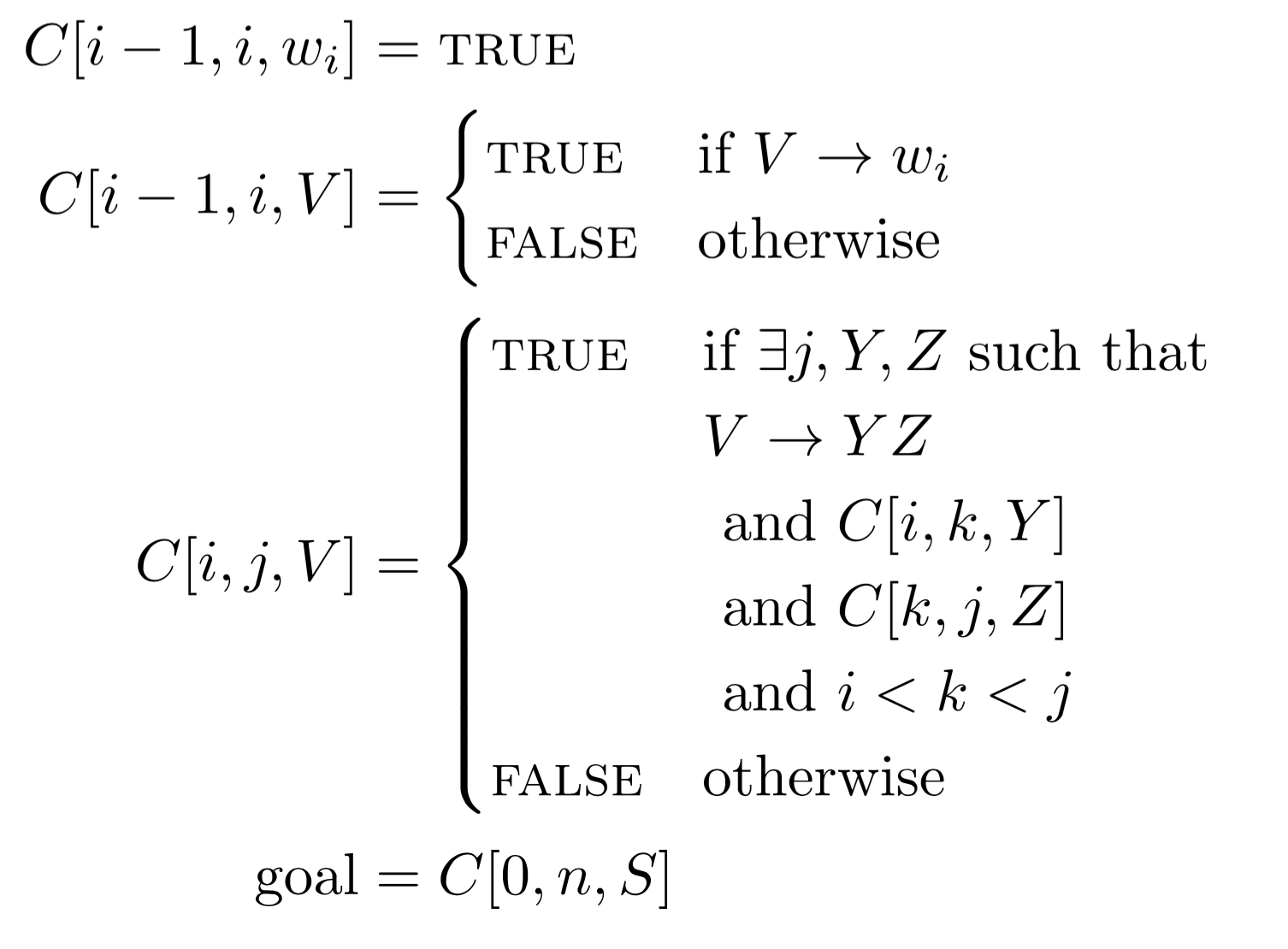
核心算法
完整算法(stanford slides)
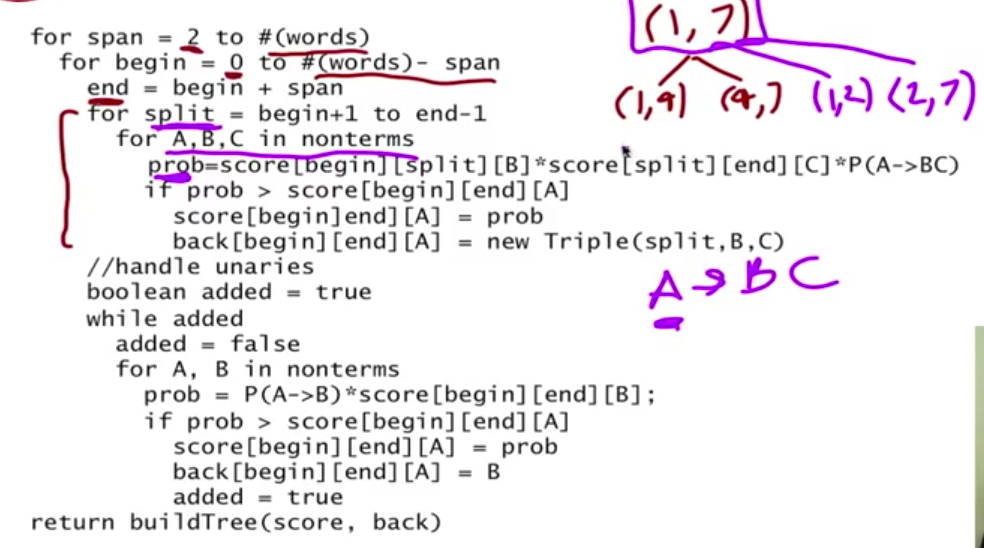
score, back 两个数组的作用是用空间换时间
worked example
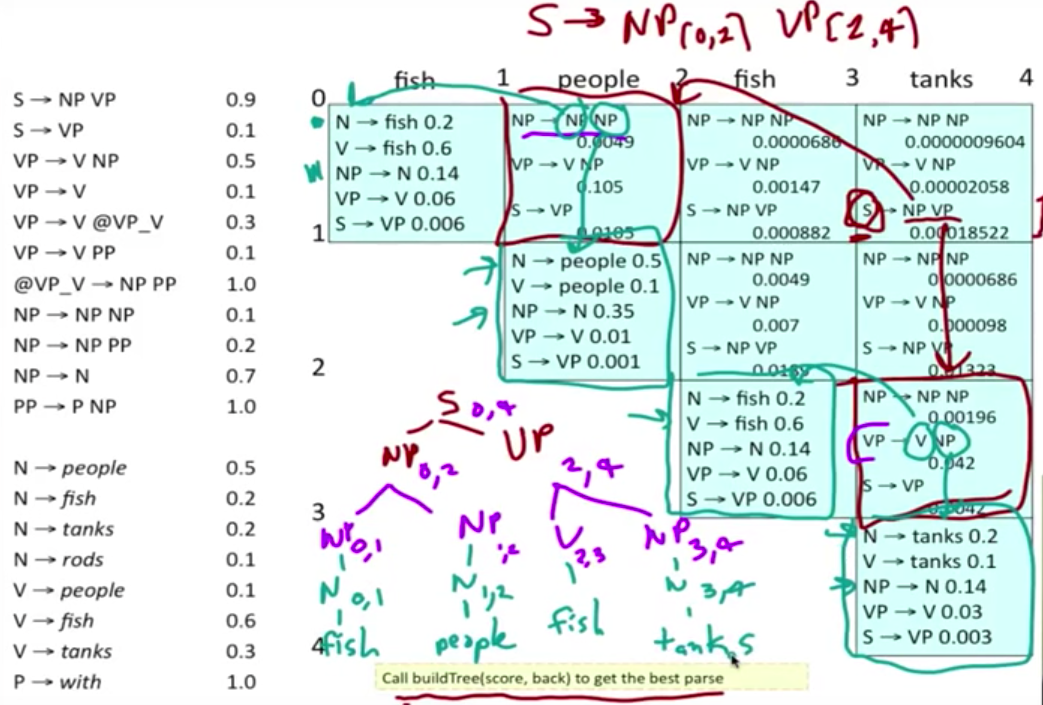
时间复杂度:
- Worst case: O(n^3*g)
- Best in worst case
- Others better in average case
Summary:
- Fills in table bottom-up, using dynamic programming
• Only builds constituents that have evidence in the input
• Never builds a constituent instance more than once
• But it builds things that cannot be used - Chomsky Normal Form is annoying
15 - 3 - CKY Parsing -Stanford NLP-Professor Dan Jurafsky & Chris Manning
15 - 4 - CKY Example-Stanford NLP-Professor Dan Jurafsky & Chris Manning
Earley
主要是一种 top-down 的剖析算法,使用动态规划表来有效存储中间结果。与 CKY 算法相比,Earley 的优势在于:
- Never build things that are useless (goes top-down),大多数情况下时间复杂度小于 $O(n^3)$
- 不用把 grammar 转化成 CNF 范式
如果输入有 N 个单词,Earley 算法会创建一个 N+1 大小的 chart,对于句子中每一个单词的位置,chart 包含一个状态表来表示已经生成的部分剖析树,在句子结尾,chart 把对于给定输入的所有可能的剖析结果进行编码,每个可能的子树只表示一次,并且这个子树表示可以被需要它的所有的剖析共享。
我们用点规则(dotted rules)来表示状态,来分隔走过的进程以及未完成的进程,每个 chart entry 可能含有三种信息:
- Completed constituents and their locations:
S → · VP [0,0]
点在成分左侧,表示这个特定的开始节点 S,第一个 0 表示预测的成分开始于 input string 的开头,第二个 0 表示点也在开头的位置 - In-progress constituents:
NP → Det · Nominal [1,2]
NP 开始于位置 1,Det 已经被成功剖析,期待下一步处理 Nominal - Predicted constituents:
VP → V NP · [0,3]
点处于两个成分右侧,表示已经成功找到了与 VP 相对应的树,而且这个 VP 横跨在整个 input string 上
从左到右走过 chart 的由 N+1 个状态组成的集合,按顺序处理每个集合中的各个状态,每一步根据具体情况将下面描述的三个操作中的一个应用于每个状态,向前移动后,不会再回溯,直到最后一个状态 S → $\alpha$ · [0,N],表示剖析成功。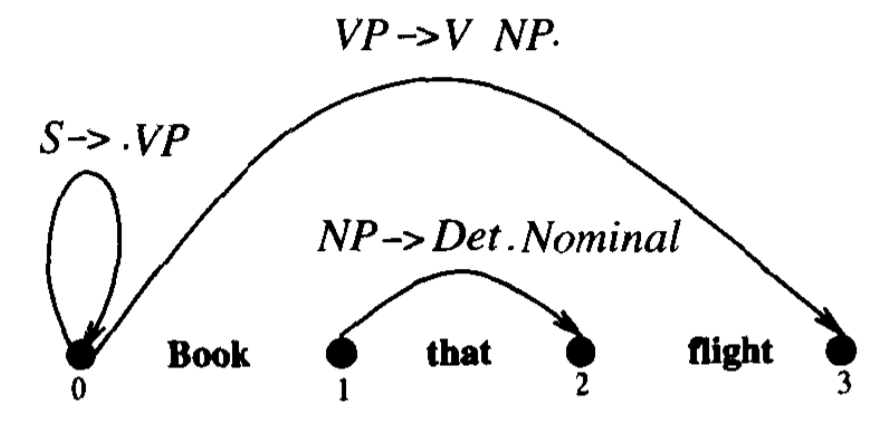
简单版的步骤
- Predict all the states you can upfront
- Read a word
Extend states based on matches
Generate new predictions
Go to step 2 - When you’re out of words, look at the chart to see if you have a winner
假设设有CFG如下:
下面以 the rat ate the cheese 为输入来演示一下 Earley 算法。
具体算法
E.g.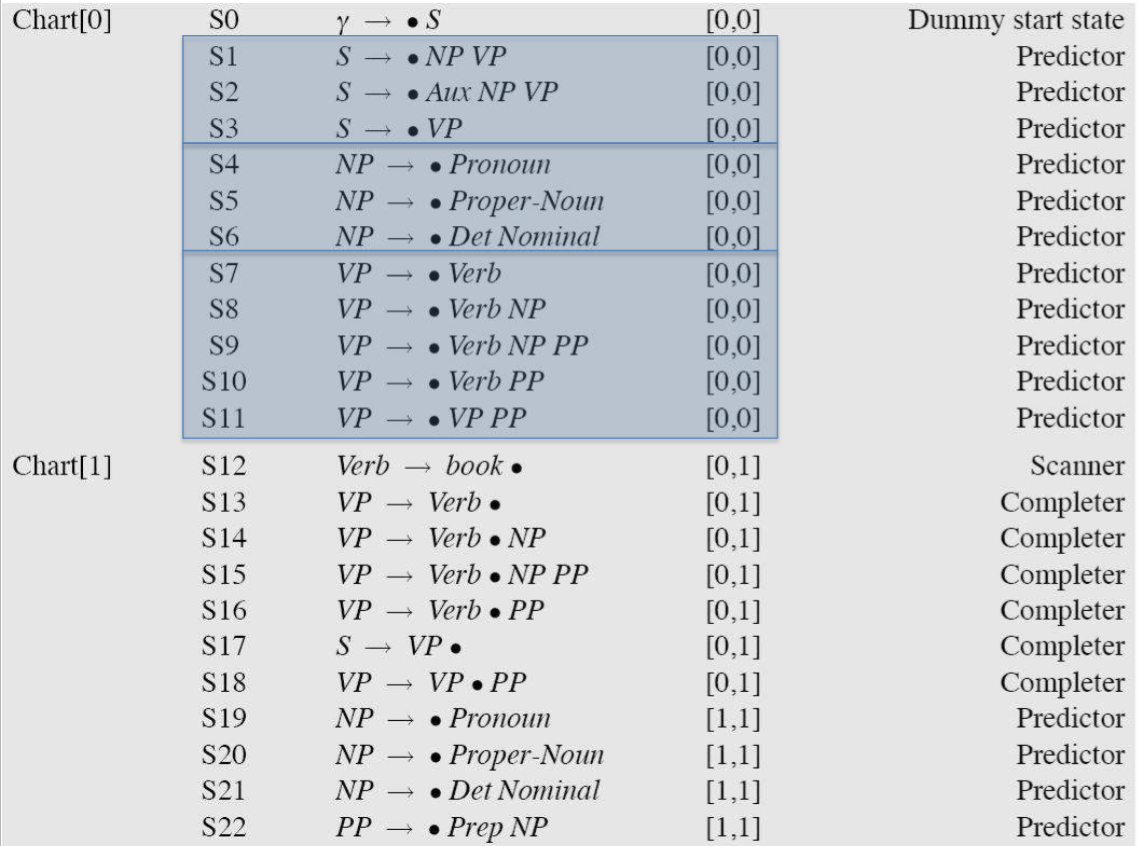

具体来看三个操作预测(Predictor)、完成(Completer)、扫描(Scanner)。
- Predictor: for non-terminals
用于 dotted-rule 中 dot 右侧为 non-terminal 符号但又不是词类范畴(part-of-speech category)的任何状态
对语法提供的 non-terminal 符号的不同展开,都创造一个新的状态,放到同样一个 chart 中,开始和结束位置与之前相同
S → · VP [0,0],用 Predictor,就是在第一个 chart entry 中增加状态 VP → · Verb, [0,0] 和 VP → · Verb NP, [0,0] - Scanner: for words
用于 dotted-rule 中 dot 右侧为词类范畴(part-of-speech category)的状态
检查 input string,把对应于所预测的词类范畴(part-of-speech category)的状态加入到 chart 中,scanner 操作后,从输入状态中造出一个新的状态
VP → · Verb NP [0,0],dot 后面是词类,所以 scanner 要在输入中寻找当前的单词,而 book 是一个 verb,与当前状态中的预测匹配,所以创造出一个新的状态 VP → Verb · NP [0,1],然后把这个新的状态加到 chart 中,跟随在当前处理过的状态之后 - Completer: otherwise
状态中的 dot 到达规则右端时,剖析算法成功找到了在输入的某个跨度上的一个特定的语法范畴,completer 的目标就是寻找输入中在这个位置的语法范畴,发现并且推进前面造出的所有状态
NP → Det Nominal · [1,3],completer 要寻找以 1 为结尾并预测 NP 的状态,找到由 Scanner 造出的状态 VP → Verb · NP [0,1],结果是加入一个新的完成状态 VP → Verb NP · [0,3]
CKY and Earley
CKY 和 Earley 都是 chart parsing 的方法,Earley 是 top-down 的,CKY 是 bottom-up 的。也有两个算法都不能解决的问题,如一致性(agreement)问题:
可以用 Combinatorial Explosion 方法来解决,如下,分开表示第一人称NP、第二人称NP、第三人称NP的规则,然而这样的组合太多了。
另外一个问题是次范畴化的问题(Subcategorization Frames),这需要依存算法来解决。
最后,来回顾一下 CFG 的假设,CFG 假设任何一个 non-terminal 符号的展开与任何其他 non-terminal 符号的展开是独立的,然而这个假设是不成立的,可以看一下下面的例子,这个问题的解决需要引入 Lexicalized grammars。
Constituency Parser Evaluation
需要有 label 数据,评价方法如下,上面的 parse tree 是标准的,下面的 parse tree 是算法产生的,我们标注每一个成分的起始和终止位置,然后比较两个 tree,看两个 tree 对应成分的起始和终止位置是否相同,计算 precision,recall,F1,和 tagging accuracy。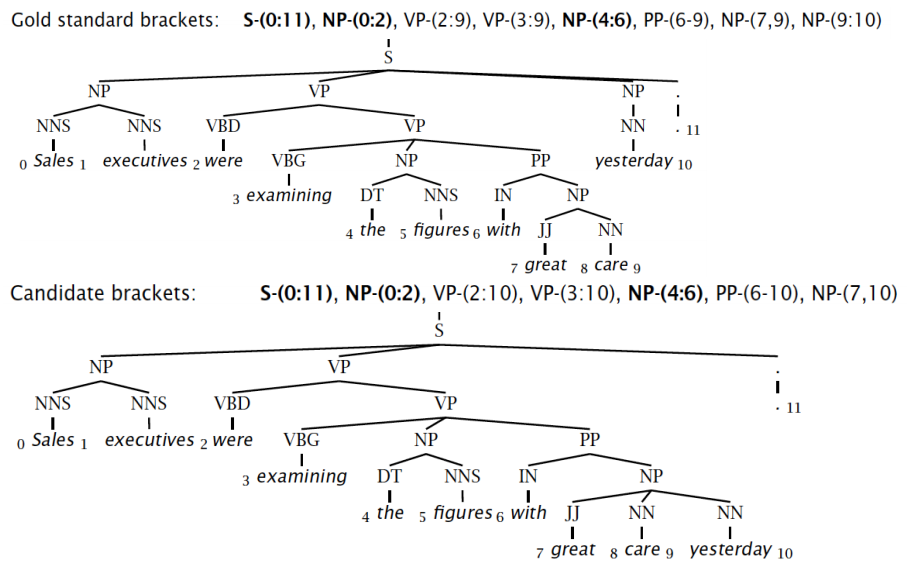
Labeled-Precision: 3/7=42.9%
Labeled-Recall: 3/8=37.5%
LP/LR-F1: 40.0%
Tagging-Accuracy: 11/11=100.0%
这种评估方式有其弱点,上层的错误会被下层持续继承,如上面的例子,只有最后一个单词 yesterday 的识别出现了错误,然而一层层传承下来,准确率就变得很低。
参考链接:
自然语言处理中的Earley算法

